3.有界则有极限
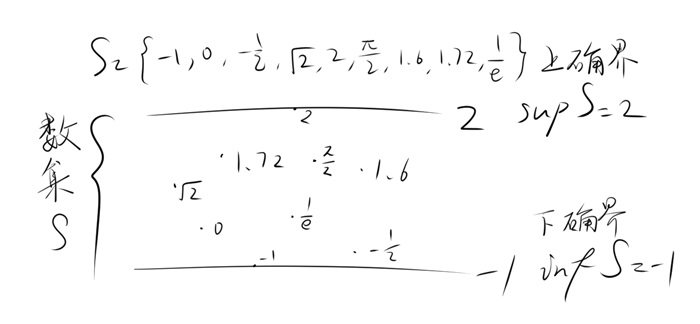
这是年试日前一天的清晨，一切如常，只不过矽一走出门就看见Isle蹲在田里，一副很专注的样子，研究着Pur麦，甚至还把麦粒摘下来嚼了几口。
“早啊。”Isle意识到矽的到来，说道。
“早……”矽说着打了个哈欠。
昨天中午，从Acdemon城回来的Isle同矽吃完午饭后又进行了一番教学，只不过这次则讲到了晚上10:20，Isle把收敛数列的四大性质——有界性、保号性、保不等式性和敛迫性完整地推到了一遍，还拓展了一些领域和确界的基本原理。
“看起来你有点困。”Isle说，拨弄着Pur麦的叶子。
“实际上我从来没有这么迟睡觉。”矽说，“毕竟魔量灯对魔量的消耗还是很大的，一个晚上要用1/4个魔量瓶的魔量，一个魔量瓶可是要花120Za（货币单位）。况且在平时，晚上呆着也没有什么事做。”
“原来魔量灯消耗这么大吗？”Isle有点惊讶，“那以后还是由我来提供照明吧。”
“你会发光？”矽突然笑了起来，问道，走进了田地。
“不。不过我来这里，身上还是带着点东西的。”Isle说着，把手伸进斗篷的口袋里，掏出了一个方块状的小东西，举高示意。他一按按钮，白色的光从其中放射出来，“量产型微型太阳能手电筒，能量转化率极高。”
“…你的故乡还真是发达呢……那么，今天学什么呢？”矽问，弯腰看了看Pur麦的生长情况，此时Aka麦还未长出地表。
“极限的存在条件，”Isle说着关掉手电筒，站起身来，“既然完成了对于性质的学习，接下来要做的就是得知极限何时存在，才能去运用它。”
“现在就开始吗？”矽问。
“没错，开始吧。”Isle说。
于是矽向屋里走去，Isle也跟在后面。
待Isle走进门时，忽然有什么东西如电光般闪过了它的脑海，阻断了神经冲动，迫使他停了下来，说：“矽，不对，我忘了什么。”
“嗯？”矽回头，看向Isle。
“对了，”Isle略带尴尬地笑着说，“极限的四则运算，我还没有讲，那就直接告诉你它的规则吧。数列极限的四则运算符合一般的四则运算法则，你能理解吧。”说着，他继续向屋内走去。
“一般的四则运算……”矽思考了一下，“lim(n→∞)(a_n+b_n)= lim(n→∞)a_n+lim(n→∞)b_n，是这样的吗？”
“不错，那么其他的你也会了吧.”Isle说。
“嗯，”矽自信地说出了答案，“lim(n→∞)(a_n*b_n)= lim(n→∞)a_n*lim(n→∞)b_n；
lim(n→∞)(a_n-b_n)= lim(n→∞)a_n-lim(n→∞)b_n；当lim(n→∞)b_n不为0时，lim(n→∞)(a_n/b_n)= lim(n→∞)a_n/lim(n→∞)b_n。”
于是两人回到了矽的卧室。
“首先我们给出一个定义：若a_n≥a_(n+1)或a_n≤a_(n+1)，那么就称a_n为单调递减或递增数列。如我们昨天的例子，数列{1/2^n}就是一个单调递减的数列。”
“这不就和单调函数的定义差不多嘛。”
“嗯，数列实际上就是一种定义域特殊的函数。”Isle说，“我们把这两种数列统称为单调数列，而我接下来要讲的就是‘单调有界定理’：在实数系中，有界的单调数列必有极限。”
“有界……指的就是有‘上界’和‘下界’的数列吧。”矽说。
“没错，”Isle说，“我们接下来就去证明这个定理。”
Isle执笔写到：“设{a_n}为有上界的递增数列。由‘确界原理’（对于非空数集S，若S有上界，则S必有上确界；下界亦同），数列{a_n}有上确界，记‘常数a=sup{a_n}（即a为{a_n}的上确界）。”
“‘a’在‘ε-N定义’也有提到过呢。”矽联想到，“难道说……”
“然后我们就要证明a是{a_n}的极限了……”
“果然！”
“……根据上确界的定义，”Isle继续证明，“即对任何α（Alpha）<a，存在a_N使得a_N>α，而在这里设ε为正整数，则α=a-ε。因为{a_n}递增，当n≥N时，有：a-ε<a_N≤ a_n。同时，因为a为a_n的一个上界，所以所有的a_n≤a<a+ε。综上所述，可以得出：a-ε<a_n<a+ε，即a_n-a<ε<a-a_n也就是|a_n-a|<ε。所以lim(n→∞)a_n=a。下界的求证也与之相同。”
“嗯，很好理解。”矽说。
“那么回想我们昨天的例子，”Isle说，“证明遮住窗户的布的面积是有限的。”
“好。”矽提笔写了起来。
“第n次时积累使用的布条量为‘1-1/2^n’(n=123…)。
∵1/2^n>0 ∴1-1/2^n<1 即‘1’为‘1-1/2^n’的上界，
又知数列{1-1/2^n}为递增数列 ∴由单调有界定理得：数列{a_n}收敛。”
“很熟练嘛，”Isle评价道，“那么接下来就让你来推一个复杂一点的：证明lim(n→∞)(1+1/n)^n存在。”
“lim(n→∞)(1+1/n)^n……”矽面对这个既底数有变量又指数有变量的式子犯难。
“难道是要用二项式定理展开吗？……对呀刚学了四则运算法则，准没错！”他突发奇想，信心满满，决定尝试，于是拿起笔：
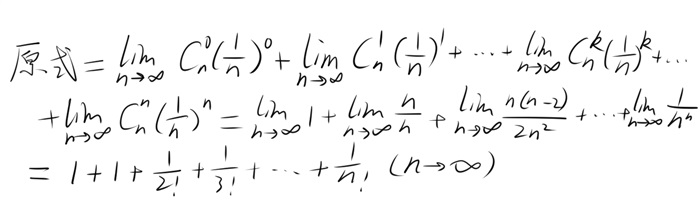
“这看起来像是一个定值。”
“想法不错，”Isle说，“不过就你来说还无法严格证明这个式子（实际上是一个无穷级数）是一个定值。你再尝试一下用单调有界定理来证明吧。”
“我再试试，”矽说，目光落在了式子上。
“单调有界定理……是不是需要不等式的知识呀。”矽想到，于是说：“有什么提示吗？”
“这里有个不等式，‘若b>a>0对任意正数n有：b^(n+1)-a^(n+1)<(n+1)*b^n*(b-a)’”Isle说，“这个公式我们以后可以推出。”
“看起来用得上。”矽转而又开始了推导，“a^(n+1)> b^n*((n+1)*a-n*b)。先把b=1+1/n>a=1+1/(1+n)代入试试看……不等式右边等于b^n((n+1)*(1+1/(1+n))-n*(1+1/n))=b^n=(1+1/n)^n，所以(1+1/(1+n))^(n+1)> (1+1/n)^n。哦，是个递增数列啊。”
“你可以再用这个公式推出它的的上界。”Isle说。
“上界……”矽说，“那令a=1，令b=1+1/n，那么1>(1+1/n)^n*(n+1-n-1)=0……不对；令b=2+2/n，那么1>2^n*(1+1/n)^n*(n+1-2*n-2)……也不行。为了把n抵消b种的常数一定要是‘1’才行，但是……”
“b取1+1/(2*n)吧。”看着被难住的矽，Isle给了他进一步的提示。
“用b=1+1/(2*n)……”矽听后继续写道，“1>(1+1/(2*n))^n*(n+1-n-1/2)=1/2* (1+1/(2*n))^n.所以2>(1+1/(2*n))^n即4>(1+1/(2*n))^(2*n)，对于任意偶数项的上界是4……”
“再根据函数单调性。”Isle继续推进。
“没错，单调性！”矽豁然开朗，“所以对于一切整数n都有4>(1+1/n)^ n，即{(1+1/n)^ n }有上界，所以它是收敛的。”
“很好，”Isle说，打了个响指，“那么我来告诉你吧，这个数列的极限是一个无理数，而且是一个‘超越数’。”
“超越数？”
“没错，就和圆周率π（pi）一样，”Isle说，“是一个不能满足任何整系数代数方程的实数。它的近似值是2.718281828459，在我们那儿用拉丁字母‘e’来表示，又称为‘自然对数的底数’，‘log_ex’又被表示为‘lnx’。”
“e……也是个很特殊的数吗？”矽问。
“没错，在以后的学习中我们说不定也会见识到它的魅力。”Isle回答道。
“我想再证明一个类似的极限练习一下。”矽说。
“lim(n→∞)(1+1/n^2)^n。”Isle说，看了看墙角的钟，挠了挠头，思考着什么，又在桌子的一旁坐下。他用铅笔在白纸上写了一些字，然后站了起来，对矽说：“我有事要先去一下A城，证明完那个极限你可以看看那边那张纸上的定理。”
“嗯，”矽专注地求着极限，Isle则飞快地离开了矽的家，疾行在前往Acdemon城的路上。
“Isle是去做些什么呢？”矽迟疑了一下，又继续自己的思考。
“柯西（Cauchy）收敛准则。”Isle想到，“对于数列{a_n}收敛的充要条件是：对任给的ε>0，存在正整数N，使得当nm>N时，有|a_n-a_m|<ε。这个定理可以联系到很多内容，但是证明它需要‘实数完备性基本定理’中区间套定理的铺垫……”
Isle离开了Zil镇，奔跑在连接着Zil镇与Acdemon城的马路上，四周是广阔的原野。他想：“实数理论这种东西就不用教给他了吧。教他数学只是为了让他获得特长的话，实数理论就交给他们——这个世界自己的力量去建立吧。”
“毕竟我所要的数学也只是为了实用呢。”
十分钟后，气喘吁吁的Isle站在A城中一家名为“WORM”的店前，走了进去。
Twost滞留之地提示您：看后求收藏（卧龙小说网http://www.wolongxs.com），接着再看更方便。
好书推荐：《等我穿上小裙子你们就完蛋啦》、《好感度破亿的病娇缠上我了》、《我穿越到了全是女生的世界》、《我穿越到全是女孩子的世界》、《夜的命名术》、《无尽宇宙探索指南》、《深空彼岸》、《玲珑塔》、《星门》、《重启灾变》、
